The field and eddy losses in the core which is made of laminated electrosheets shall be computed.
Download as PDF Download NX Files
Initial Situation
Demo Transformer
The problem is a simple one phase transformer as shown in the next picture. Goal is to apply alternating current on the primary coil and a resistor as load condition on the second coil. The field and eddy losses in the core shall be computed. The core is made of laminated electro sheets. The results shall be carried out for different lamination thicknesses: We want to use a sweep from 0.1 until 1 mm thickness.
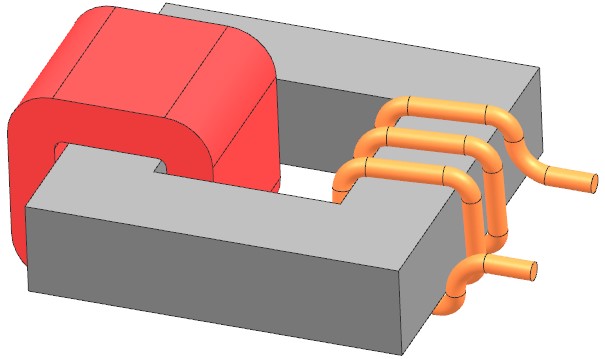Picture: CAD model of the transformer to analyze
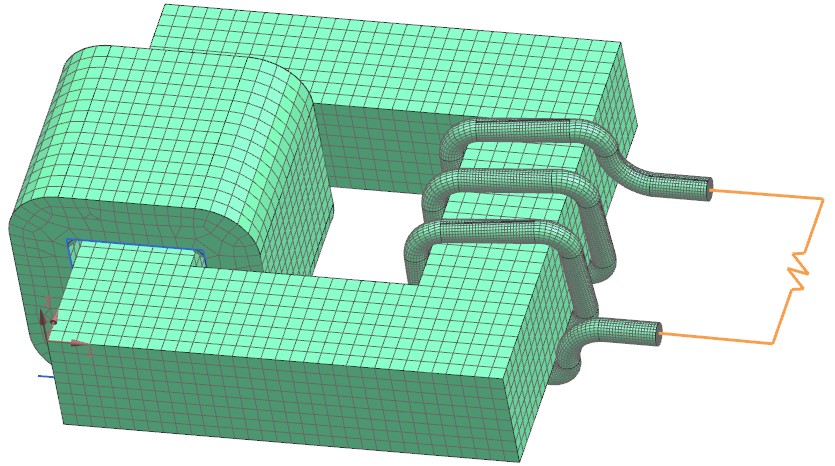Picture: FEM Model of the Transformer
Most Elements are 3D Hexahedral. The load on the secondary coil is modeled by a 1D Circuit.
Some given dimensions are these:
- Transformer length: 40 mm,
- Primary coil number windings: 237
- Primary coil fill factor: 0.6
- Secondary coil number windings: 3
Appropriate Method
3D Magnetodynamic Frequencydomain with Circuits
This kind of problem is solved in NX Magnetics using a 3D Magnetodynamic Frequencydomain solution type and additionally a circuit network for the load on the secondary coil. Of course there are other possibilities too. Alternative approaches would be to compute in time domain which would allow to take into account nonlinear material conditions. Also 2D analysis would be convenient. Next pictures show the mesh and some details about it.
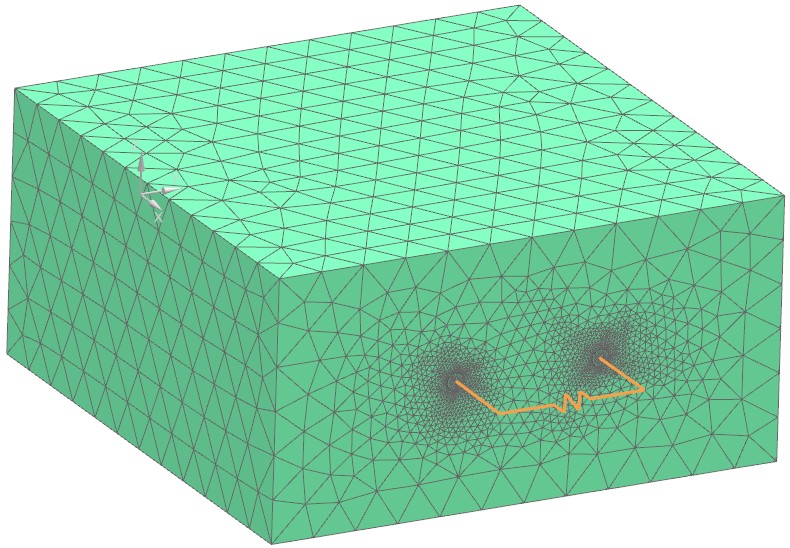Picture: There is an Air Box meshed around the transformer in which the electromagnetic field is computed
The meshing is done next. We use hexahedral elements for both the coils and the plates. These elements lead to best results in finite element solutions. These elements can easily be connected to the outside air that will be meshed by tets using pyramids in the transition area.
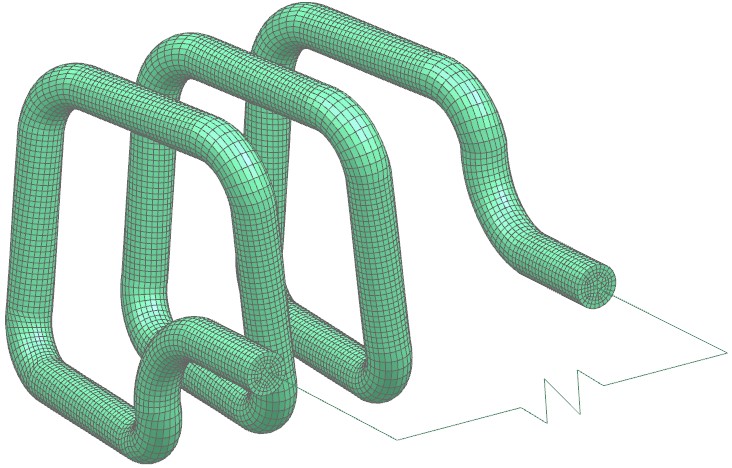Picture: Detail view on the secondary coil which is modeled as a massive conductor. All Eddy Currents, Skin-Depth and Proximity Effects in the 3D model are captured by this meshing method.
Picture: Detail view on the primary coil.
This coil is modeled by a stranded approach which means that each element has a vector (see next picture) to define the winding direction
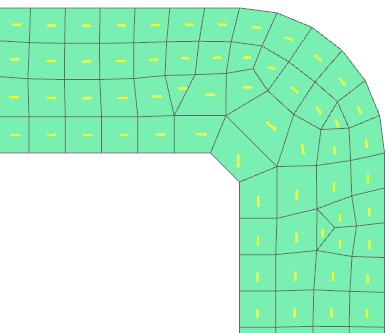Picture: Definition of the winding directions
To capture the effect of lamination sheets we use a homogenization technique that takes into account how eddy currents behave in case of thin sheets. Because the eddy currents effects the field also other result quantities will be influenced by this. In NX Magnetics this technique is applied by assigning a coordinate system for the stack direction as seen in the next picture.
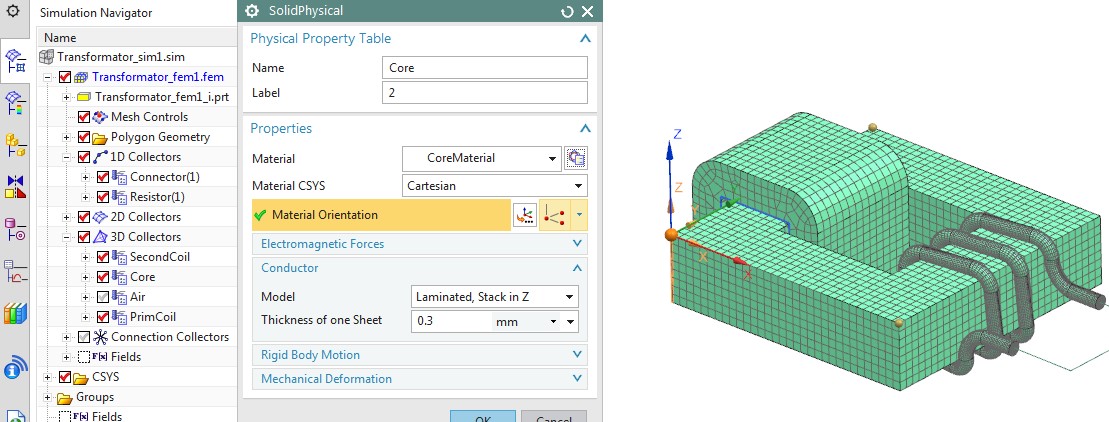Picture: The application of Lamination Effects on the Core
As described in the task we will carry out simulations with different thicknesses. We expect the losses will increase with larger thicknesses.
The circuit is modeled by a 1 dimensional element. See the NX Magnetics dialog in the next picture.
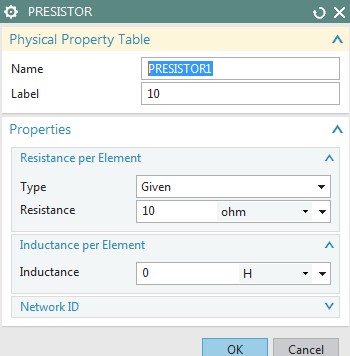Picture: The application of Ohm Resistance to the Circuit Element
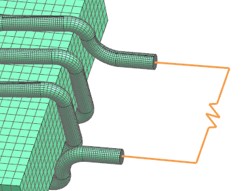Picture: The Circuit Element.
In the NX Simulation file we set up a Magnetodynamic solution in frequency domain at 50 Hz. We call it LaminationSweep because we want to run a Parameter Sweep over several thicknesses of the sheet. Next picture shows the solution dialog and the requested outputs.
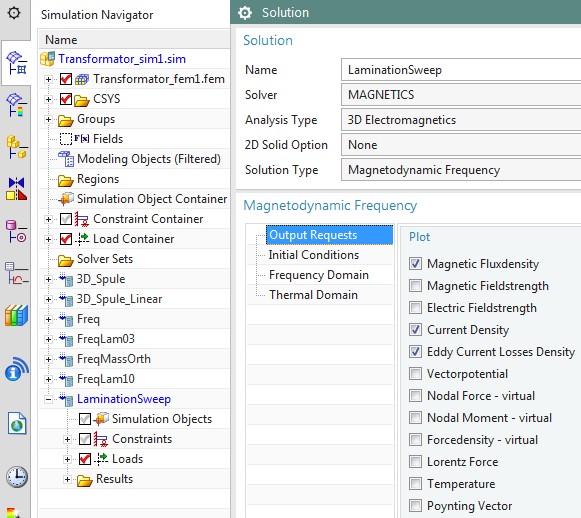
Picture: The NX Magnetics dialog for the solution and the Output Requests
We apply a peak current of 0.5 Amperes. Then we set up the parameter sweep. We will vary the sheet thickness starting at 0.1 mm and ending at 1 mm with a step size of 0.1. The ParameterSweep dialog is show in the next picture.
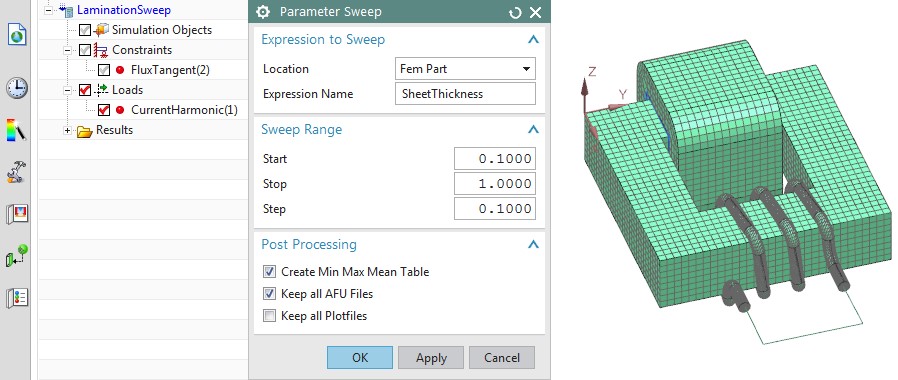Picture: The NX Magnetics dialog for the Parameter Sweep
The solution time depends on the computer being used. I can vary between 5 and 20 minutes.
Result
Losses Table, B Field and Eddy Currents
After some minutes the parameter sweep has finished and all results can be discussed. We start with the eddy current losses on the core which is our main result. In case of parameter sweeps this result comes out of the system by a textual table which can be displayed in Excel for example. See next picture.
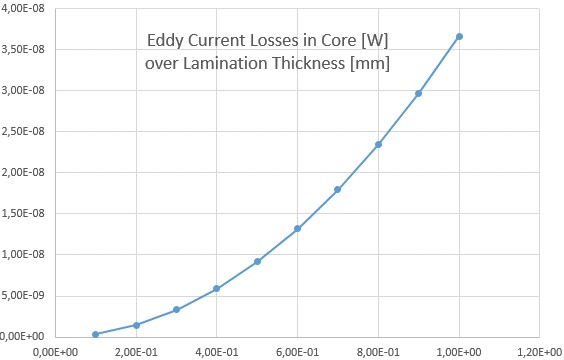Picture: The computed Eddy Current Losses in the Core as they vary with the Lamination Thickness
The field solution allows detailed insight in the behavior of the magnetic, electric and the eddy current fields. All results can be plotted in real, imaginary or other combinations. Such plots help the user to understand how geometric details influence the result. The next picture shows the magnetic Flux density.
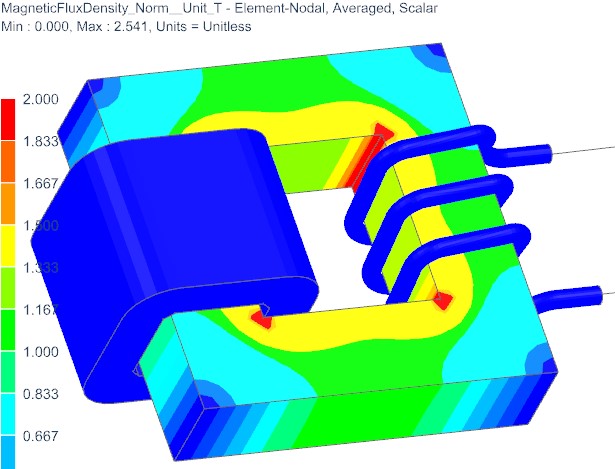Picture: B Field on Transformer
Picture: B Field (Vector View) on Transformer
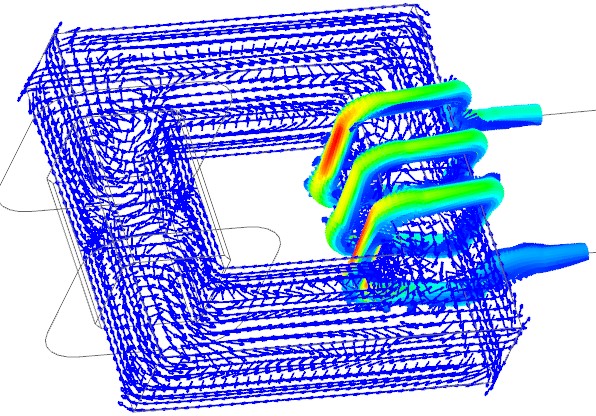Picture: Eddy Currents on Transformer
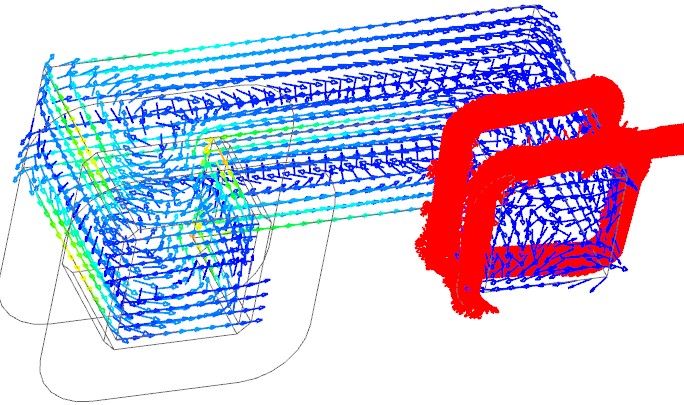Picture: Eddy Currents on Transformer
Performance, Statistics:
- Total number of elements: 225644
- Total number of nodes: 95955
- Number of Hexa elements: 62900
- Number of Tetra elements: 140987
- Solution time per Sweep Step: 2 min
- CPU: 205 s.
- Memory used: 930 Mb
- Computer: Intel Pentium i7, 4 cores
